(译)函数式编程增强库Vavr初探(二)
本文是翻译Vavr官方文档的序章,上一篇的使用指南介绍了Vavr中的主要组件的定义和使用示例。其中也出现了一些函数式编程的概念,如函数副作用、引用透明性、持久化集合、不可变数据结构等等,在序言中都有更进一步的阐述。
1. 序章
Vavr(过去叫Javaslang)是一个为Java8+而生的函数式库,它提供了持久化数据类型和函数式控制结构。
1.1. 用Vavr实现Java8的函数式数据结构
Java8的lambdas (λ)能让我们构建出很棒的API’s,这些API极大的提升了语言的表现力。
Vavr利用基于函数式模型的lambdas创造了一系列的新特性,其中一个就是函数式集合库,旨在替换Java中的标准库。
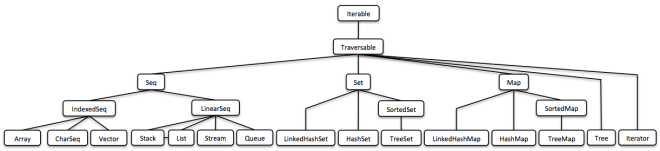
(这只是一张鸟瞰图,接下来会有更易于阅读的版本。)
1.2. 函数式编程
在探讨细节之前,我想先讲解一些基础知识。解释一下我为什么会设计Vavr,特别是新的Java集合类。
1.2.1. 副作用
Java应用通常都有大量的副作用。它们改变了某种状态,可能是外界的(程序以外的)。常见的副作用是原地改变对象或者变量,打印到控制台、写到日志文件或者数据库。如果副作用以非预期的方式影响了我们程序的语义,那就认为它是有害的。
例如,一个函数抛出了异常且这个异常是interpreted,它就被认为是一个影响程序的副作用。而且,异常类似于非本地的go-to语句,它们会破坏正常的控制流。不管怎么说,实际的应用确实会产生副作用。
int divide(int dividend, int divisor) {
// throws if divisor is zero
return dividend / divisor;
}在函数环境下,可以用Try来封装副作用使我们(的程序)处于一个良好的状态:
// = Success(result) or Failure(exception)
Try<Integer> divide(Integer dividend, Integer divisor) {
return Try.of(() -> dividend / divisor);
}上面这个版本的divide方法不会再抛出任何异常,我们利用Try类型显式的显示了可能的失败。
1.2.2. 引用透明性
一个函数,或者更笼统的说一个表达式,对它的调用如果能用它的值替换而不影响程序本身的行为,那就称之为引用透明性。简单来讲,给定相同的输入总能得到相同的输出。
// not referentially transparent
Math.random();
// referentially transparent
Math.max(1, 2);如果(函数中)涉及的所有表达式都是引用透明的,则称该函数为纯函数 。一个由纯函数组成的应用大概率在编译后就可以直接运行,这也很容易解释。单元测试变得易于编写,而调试则成为了过去式。
1.2.3. 对值的思考
Clojure语言创始人Rich Hickey,曾做过一个很棒的演讲The Value of Values。其中最有趣的值就是不可变值,主要原因是不可变值
天然是线程安全的,因此也无需同步
有关于equals和hashcode都是稳定的,所以(不可变值)也是可靠的哈希键
无需克隆
当被用在未经检查的协变[1]转换(Java特有的)中时也能表现得类型安全
用不可变值搭配引用透明性函数是使Java变得更好的关键,Vavr则提供了必要的控件和集合以在日常的Java编程中达成这一目标。
1.3. 果壳中的数据结构
Vavr的集合库包含了一组丰富的基于lambda之上的函数式数据结构,唯一个与Java原生集合共享的接口是Iterable。(没有共享其他接口的)主要原因是基于Java集合接口的更改器方法[2]无法返回一个底层集合类型的对象。
下面来看看不同类型的数据结构,我们会知道为什么这(不共享集合接口)是非常必要的。
1.3.1. 可变数据结构
Java是一门面向对象编程语言。我们通过封装对象的状态来达到数据隐藏的目的,然后提供更改器方法控制这种状态。Java collections framework (JCF) 就是基于此种思想构建的。
interface Collection<E> {
// removes all elements from this collection
void clear();
}现在我会把void的返回类型理解为一种异味。它就是副作用产生的证据,会使得状态发生变换。共享可变状态是一个造成失败的主要来源,不仅仅在并发环境中。
1.3.2. 不可变数据结构
不可变数据结构被创建后就无法更改。在Java的上下文中,它们以集合包装器的形式被广泛应用。
List<String> list = Collections.unmodifiableList(otherList);
// Boom!
list.add("why not?");有各种各样的库提供了类似实用的方法给我们。(这些方法)返回的结果总是一个特定集合的不可变视图,而且通常在我们调用一个更改器方法后在运行时抛出(异常)。
1.3.3. 持久化数据结构
一个持久化数据结构在被修改时,会保留它以往的版本,也因此形成了事实上的不可变。完全地持久化数据结构允许对任何版本进行更新和查询。
许多操作只会执行很小的改动,仅仅拷贝上一个版本并不会变得高效。要节省时间和内存,确认两个版本之间的相似之处并尽可能多的共享数据就显得尤为重要。
这种模型不会强制任何实现细节,此时就该函数式数据结构登场了。
1.4. 函数式数据结构
也被称作纯 函数式数据结构,它们是不可变且持久化的。函数式数据结构的方法都是引用透明的。
Vavr拥有许多很常用的函数式数据结构,接下来会举例进行深入讲解。
1.4.1. 链表
最受欢迎当然也是最简单的一种函数式数据结构就是 (单)链表,它有一个头元素和一个尾列表。链表的行为类似于遵循后进先出 (LIFO)方法的栈。
在Vavr里我们可以像这样来实例化一个列表:
// = List(1, 2, 3)
List<Integer> list1 = List.of(1, 2, 3);列表中的每一个元素都形成了一个独立的节点,最后一个元素的尾部指向Nil,一个空的列表。[3]

这使得我们可以在列表的不同版本之间共享元素:
// = List(0, 2, 3)
List<Integer> list2 = list1.tail().prepend(0);新的头元素0被链接到原列表的尾部[4],原来的列表则保持不变。
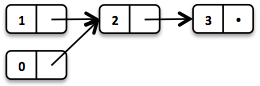
这些操作都会在常数时间内运行,换句话说就是与列表的大小无关。大部分其它操作都是线性时间,在Vavr里面会通过接口LinearSeq来表示,我们可能已经从Scala中了解过了。
如果我们需要能在常数时间内执行查询的数据结构,Vavr提供了Array和Vector,它们都拥有随机存取的能力。
Array类型由Java对象数组支持,插入和删除操作都是线性时间。Vector(的时间开销)则介于Array和List之间,它在随机存取和修改时表现的都很不错。
实际上链表也可以用来实现队列数据结构。
1.4.2. 队列
一个很高效的函数式队列可以基于两个链表来实现。front链表持有出队的元素,rear链表持有入队的元素,入队和出队操作都是O(1)的时间复杂度。
Queue<Integer> queue = Queue.of(1, 2, 3)
.enqueue(4)
.enqueue(5);队列由3个元素初始化,还有两个元素在rear列表中排队。
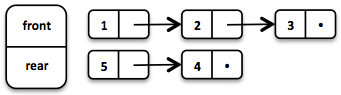
如果front列表在出队时元素耗尽,那么rear列表会被翻转成为新的front列表。
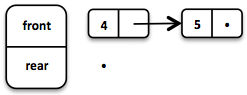
一个元素出队时我们会得到第一个元素和剩余队列组成的一对数据。必须返回这个队列的新版本,因为函数式数据结构是不可变且持久化的,原队列不应当受影响。
Queue<Integer> queue = Queue.of(1, 2, 3);
// = (1, Queue(2, 3))
Tuple2<Integer, Queue<Integer>> dequeued = queue.dequeue();当队列为空时会发生什么?这时dequeue()方法会抛出NoSuchElementException,用函数式方式来做的话我们更期望返回一个可选结果。
// = Some((1, Queue()))
Queue.of(1).dequeueOption();
// = None
Queue.empty().dequeueOption();一个可选结果可以被进一步处理,不管它是否为空。
// = Queue(1)
Queue<Integer> queue = Queue.of(1);
// = Some((1, Queue()))
Option<Tuple2<Integer, Queue<Integer>>> dequeued = queue.dequeueOption();
// = Some(1)
Option<Integer> element = dequeued.map(Tuple2::_1);
// = Some(Queue())
Option<Queue<Integer>> remaining = dequeued.map(Tuple2::_2);1.4.3. 有序集合[5]
有序集合是比队列使用得更频繁的一种数据结构。我们使用二叉搜索树以函数式方式给它们建模,这些树由一些节点组成,每个节点有一个值且最多只能拥有两个孩子节点。
我们会在排序的情况下 - 使用一个元素比较器来表达,构建二叉搜索树。任何给定节点的左子树的值都严格地小于当前给定节点的值,而所有右子树的值则严格地大于。
// = TreeSet(1, 2, 3, 4, 6, 7, 8)
SortedSet<Integer> xs = TreeSet.of(6, 1, 3, 2, 4, 7, 8);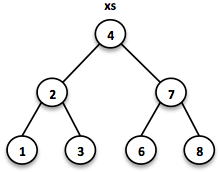
这棵树的查询时间复杂度为O(logn)。我们从根节点开始搜索,并判断是否找到了目标元素。由于所有的值是整体有序的,所以我们知道下一步该从何处进行搜索,是这棵树的左分支还是右分支。
// = TreeSet(1, 2, 3);
SortedSet<Integer> set = TreeSet.of(2, 3, 1, 2);
// = TreeSet(3, 2, 1);
Comparator<Integer> c = (a, b) -> b - a;
SortedSet<Integer> reversed = TreeSet.of(c, 2, 3, 1, 2);大部分树的操作本质上都是递归。插入函数和搜索函数很类似,当一条搜索路径抵达终点时,会创建一个新节点,然后整个路径会重建到根节点,(在此期间会)尽可能的引用现有的子节点。因此插入操作会花费O(logn)的时间和空间。
// = TreeSet(1, 2, 3, 4, 5, 6, 7, 8)
SortedSet<Integer> ys = xs.add(5);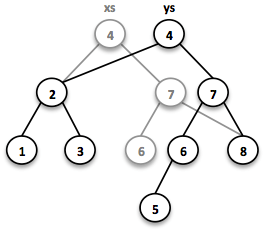
为了保持二叉搜索树的性能特点,它需要保持一个平衡。所有从根节点到叶子节点的路径需要在大体上保持等长。
在Vavr里面我们基于红黑树实现了一个二叉搜索树,它使用一种特殊的着色方式来使得二叉树在插入和删除节点时保持平衡。
如想了解更多关于本章节主题的内容,请查阅Chris Okasaki的书籍 Purely Functional Data Structures。
1.5. 集合的状态
一般来说,我们看到的是目前编程语言的趋同。优秀的特性会保留,反之则会消亡。但是Java不同,它注定要一直向后兼容,这是一种优势但也会延缓发展速度。
Lambda拉近了Java和Scala的距离,当然他们还是不一样的。Scala之父,Martin Odersky,最近在他的BDSBTB 2015 keynote里就提到了Java8集合的状态。
他把Java的Stream形容成一种很花哨的迭代器。Java8 Stream API是一个lifted集合的示例,它所做的就是定义一次计算并在另一个明确的步骤中把它link到一个特定的集合。
// i + 1
i.prepareForAddition()
.add(1)
.mapBackToInteger(Mappers.toInteger())这就是新的Java8 Stream API的工作机制,它就是一个在人所熟知的Java集合之上的计算层。
// = ["1", "2", "3"] in Java 8
Arrays.asList(1, 2, 3)
.stream()
.map(Object::toString)
.collect(Collectors.toList())Vavr则深受Scala的启发。上面的例子在Java8中本应该是这样的:
// = Stream("1", "2", "3") in Vavr
Stream.of(1, 2, 3).map(Object::toString)过去一年我们在实现Vavr集合库上面付出了很大的努力,它包含了绝大多数的被广泛使用的集合类型。
1.5.1. Seq
我们通过实现序列类型来开启我们的旅程。在上面我们已经详述了链表,之后的Stream是一个惰性链表。它允许我们处理可能的无限长度的元素序列。
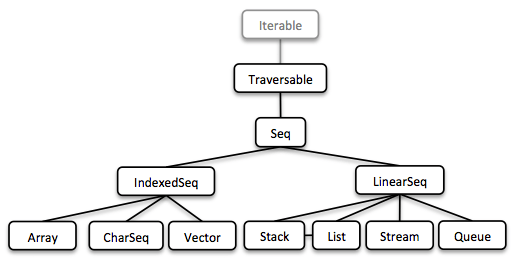
所有集合都是迭代器,因此能够被用在增强型for语句里面:
for (String s : List.of("Java", "Advent")) {
// side effects and mutation
}我们也可以通过内部化循环并使用lambda注入行为来达到同样的效果:
List.of("Java", "Advent").forEach(s -> {
// side effects and mutation
});总之,如前所见我们更期望的是返回一个带值的表达式而不是不返回任何东西的语句。通过一个简单的例子,我们马上就能意识到这种语句会带来干扰并且会把一个整体的东西分割开。
String join(String... words) {
StringBuilder builder = new StringBuilder();
for(String s : words) {
if (builder.length() > 0) {
builder.append(", ");
}
builder.append(s);
}
return builder.toString();
}Vavr集合提供了很多操作底层元素的函数,这让我们可以用很简洁的方式来表达某些事物:
String join(String... words) {
return List.of(words)
.intersperse(", ")
.foldLeft(new StringBuilder(), StringBuilder::append)
.toString();
}Vavr可以用各种不同的方式来实现许多目标。在这里我们可以通过缩减整个方法体来使列表实例上的函数调用变得更流畅,甚至可以移除这个方法然后直接用我们的列表来获取计算结果。
List.of(words).mkString(", ");在实际应用中我们可以借此大幅减少代码行数,也降低了出现bug的风险。
1.5.2. Set和Map
序列固然很棒,但就完整性来讲,一个集合库也需要不同类型的Sets和Maps。
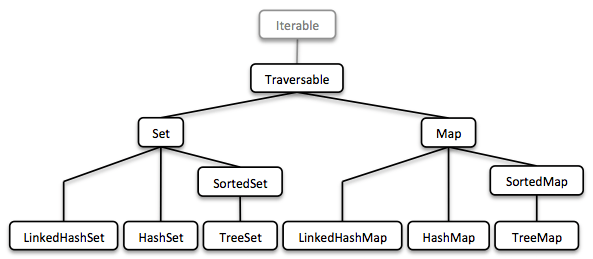
我们已经描述过如何通过二叉搜索树为有序集合进行建模,而一个有序的Map也不过是一个包含键值对且对键进行了排序的有序集合。
HashMap的实现是依赖于Hash Array Mapped Trie (HAMT),对应的HashSet也是依赖于一个包含键键对(key-key pairs)的HAMT。
我们的Map没有一个特殊的Entry类型来表示键值对,作为替代使用的是Vavr中的Tuple2。一个Tuple[6]中的字段总是可枚举的。
// = (1, "A")
Tuple2<Integer, String> entry = Tuple.of(1, "A");
Integer key = entry._1;
String value = entry._2;Maps和Tuples在Vavr中广泛被应用。把Tuples作为处理多值返回类型的一种通用方式已经是惯例了。
// = HashMap((0, List(2, 4)), (1, List(1, 3)))
List.of(1, 2, 3, 4).groupBy(i -> i % 2);
// = List((a, 0), (b, 1), (c, 2))
List.of('a', 'b', 'c').zipWithIndex();在Vavr里,我们会通过实现99 Euler Problems来考察以及测试我们的库,这是一个很棒的概念性验证,请不要吝啬给我们的库推送PR。